|
|
|
|
In this project, we will attempt to implement a physics-inspired algorithm for simulating building and statue erosion due to physical or chemical effects. As an example, given a mesh, we could simulate weathering via sandstorms by indenting mesh faces when they are impacted by simulated sand particles.
In the past week, we have performed our literature review and have decided that our approach outlined in the project proposal was sufficient. We were unable to find physically realistic data that's related to our project, such as the distribution of velocities in a windstorm or the composition of rocks like that of Delicate Arch. We've decided to proceed with our project by using "guess and check" to find combinations of parameters that make our results appear interesting.
We are using previous codebases from this course to mediate our work. From Project 2, we are modifying the Mesh Editor. We want to introduce a property of "hardness" at each point, which will be randomly assigned. Harder vertices will require more energy to be affected. If some threshold relationship between energy and hardness is met, the vertex will indent some amount in the direction at which the particle came. We have not yet been able to implement hardness yet, but it will be an important part of our project that gives us interesting results. For now, we set all parts of the mesh to have equal hardness.
We create a new Particle class within halfEdgeMesh.h to account for the particles that will cause the mesh to indent. We found that we couldn't make a new class, because it would need to include halfEdgeMesh.h to use the various iterators. However, halfEdgeMesh would also have to include the particle class, so this became circular. Ultimately, we decided simply to make the Particle class within the halfEdgeMesh.h file. Within this particle mass, we define its mass and velocity, which will dictate its energy via the energy equation E = (1/2)*m*v^2. Additionally, the class accounts for the source position of the particle and its direction. Currently, we generate a random point on a plane in front of the mesh and a random point on a plane behind the mesh which dictates the direction of the ray. We follow this vector until it intersects with the mesh. From there, we calculate the barycentric coordinates to the nearest vertices. Currently, for simplicity and proof-of-concept, we assume no bouncing so that the barycentric field of the class will contain only one set of barycentric coordinates. Ultimately, when we implement nonzero bouncing of the particle, the intersection field will contain a list of barycentric coordinates.
We had to also edit meshEdit.cpp from Project 2 so that we can control the simulation. We press 'p' to increment by one timestep, at which point a set of particles is generated. Currently, we are using 1000 particles per timestep. Each particle is checked to see if it intersects the mesh, and if so, where it intersects. The vertices of the intersecting face are displaced in the direction of the particle's motion proportionally to their corresponding barycentric coordinates.
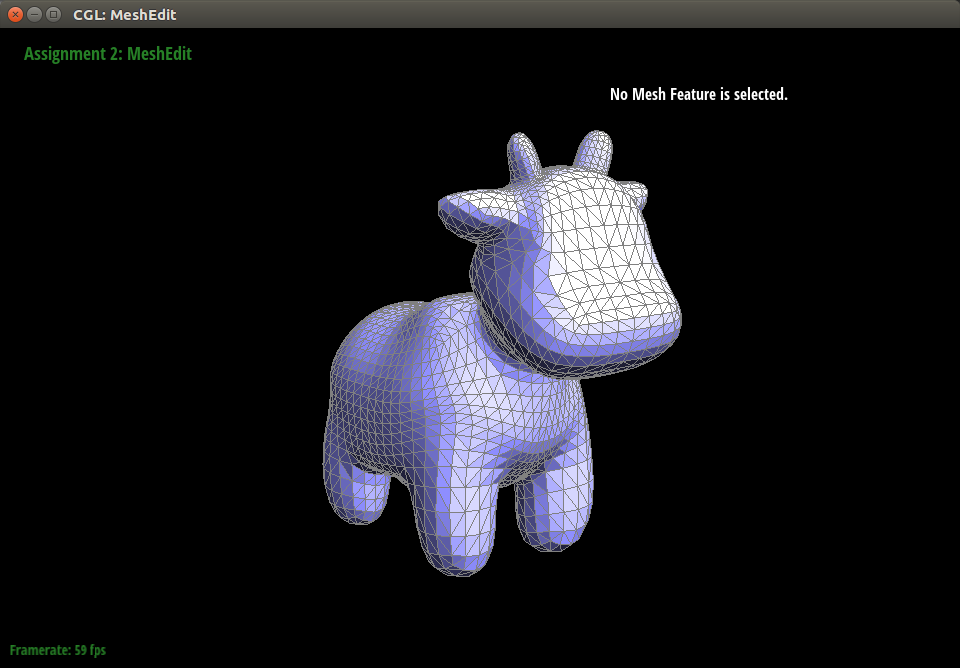
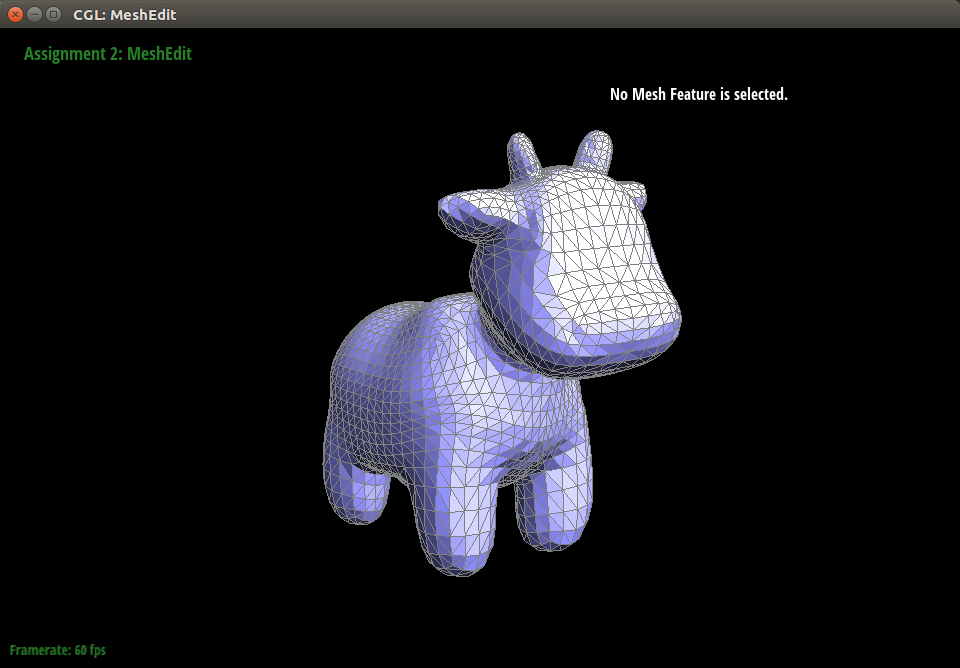
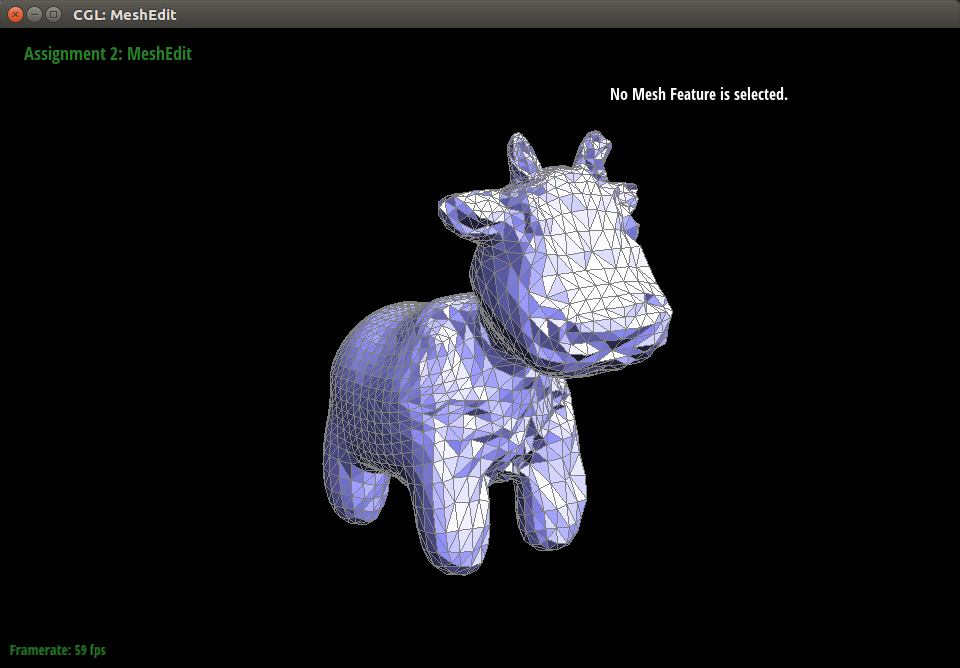
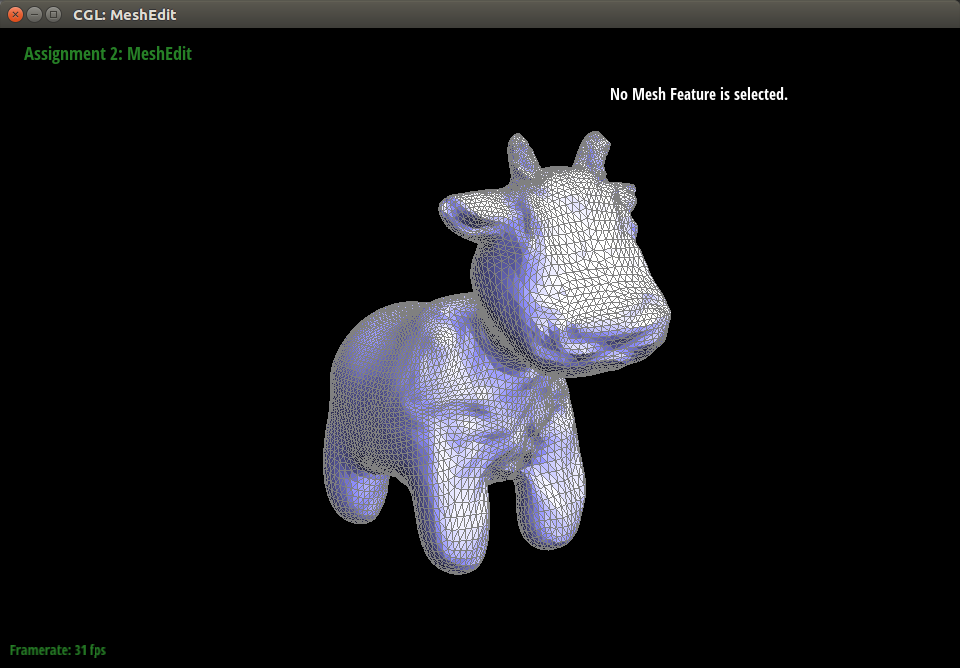
We find our results to be satisfactory at this stage of the project. For testing, we have been using the cow mesh from class. Below are images of it during various stages of being hammered by particles.

|

|

|

|
A summary of our work so far can be found at these slides here. A video demonstration can also be watched here.